The Art of Dithering and Retro Shading for the Web

Dithering techniques

Dithering originated as an early graphics technique to trick the viewer's brain into seeing more color or smoothness in gradients/shadows that the machines back in the day could output by intentionally introducing noise on top of an image or a render. Color palettes were very limited back then, thus relying on techniques like these was vital for game designers to realize their vision. This gave, as a result, a unique look and feel to games and media from that specific moment in time where computers became ubiquitous, but advanced graphic capabilities were not yet there.

Today, dithering is more an artistic choice than a workaround. Many artists or game designers use this technique as a creative outlet to give their work a unique retro vibe, calling out to that early gaming era, or work within the realms of self-imposed limits in colors. Some great examples of such use of dithering include:

• Basement Studio's Basement Chronicle game: a well-executed point-and-click game that reminds me a lot of my own early gaming experience.
• @loackme's art, which I'm an absolute fan of.
• @aweusmeuh's use of the original Game Boy camera for experimental photography which features a sublime dithering effect.

The latter is how we will approach dithering in this blog post: to give our React Three Fiber/Three.js projects a unique style! In this first part, we'll explore how the dithering technique works, implement it as a shader, and build a first iteration of a custom dithering post-processing effect that we can apply on top of any 3D scene.

A first pass at dithering in React Three Fiber

For this project, we'll create a custom post-processing effect. As we did for the Moebius stylized shader, relying on post-processing will allow us to apply a shader to an already rendered scene and alter its style like adding an "image filter" to a photo.

To create a custom effect, we will:

1. Declare a class that extends from Effect
2. Define our fragment shader and call it from the parent constructor using the super keyword.
3. Define the set of uniforms we will need for our effect.
4. Call the wrapEffect function from @react-three/post-processing with our effect class as an argument. This will allow us to use our effect as a JSX component within EffectComposer.

1
import { OrbitControls, OrthographicCamera, useFBO } from '@react-three/drei';
2
import { Canvas } from '@react-three/fiber';
3
import { wrapEffect, EffectComposer } from '@react-three/postprocessing';
4
import { Effect } from 'postprocessing';
5
import { Suspense, useRef, useState } from 'react';
6
import { v4 as uuidv4 } from 'uuid';
7
import fragmentShader from './fragmentShader.glsl';
8

9
class RetroEffectImpl extends Effect {
10
  constructor() {
11
    super('RetroEffect', fragmentShader, {
12
      uniforms: new Map([]),
13
    });
14
  }
15
}
16

17
const RetroEffect = wrapEffect(RetroEffectImpl);
18

19
const Retro = () => {
20
  const mesh = useRef();
21

22
  return (
23
    <>
24
      <mesh receiveShadow castShadow>
25
        <torusKnotGeometry args={[1, 0.25, 128, 100]} />
26
        <meshStandardMaterial color="cyan" />
27
      </mesh>
28
      <EffectComposer>
29
        <RetroEffect />
30
      </EffectComposer>
31
    </>
32
  );
33
};

As a first step to building our effect, we'll start with a simple luminance-based white noise dithering. The idea behind this is to:

• Look at the luminance of each pixel.
• Compare it to a random number (hence the "white noise" in the name).
• Output a white or black pixel based on whether the luminance falls above or below said random number.

1
float random(vec2 c) {
2
  return fract(sin(dot(c.xy, vec2(12.9898, 78.233))) * 43758.5453);
3
}
4

5
vec3 whiteNoiseDither(vec2 uv, float lum) {
6
  vec3 color = vec3(0.0);
7

8
  if (lum < random(uv)) {
9
      color = vec3(0.0);
10
  } else {
11
      color = vec3(1.0);
12
  }
13

14
  return color;
15
}
16

17
void mainImage(const in vec4 inputColor, const in vec2 uv, out vec4 outputColor) {
18
  vec4 color = texture2D(inputBuffer, uv);
19

20
  float lum = dot(vec3(0.2126, 0.7152, 0.0722), color.rgb);
21
  color.rgb = whiteNoiseDither(uv, lum);
22

23
  outputColor = color;
24
}

You can observe the effect that this code would yield on the widget below which re-implements a similar process:

Doing this will result in a grayscale version of our scene where any pixel not purely black or white will be dithered tricking our brains into seeing more shades of gray. The demo below shows the effect applied on top of a simple React Three Fiber scene:

Ordered Dithering and Bayer Matrix

The effect we just built works, but it relies on white noise for its dithering threshold, leading to a messy result. We can bring order to all this (🥁) using a technique commonly known as ordered dithering due to the ordered pattern it yields when applied.

This technique relies on a threshold map defined via a Bayer Matrix that contains values used to determine whether we should adjust the color of a given pixel to black or white.

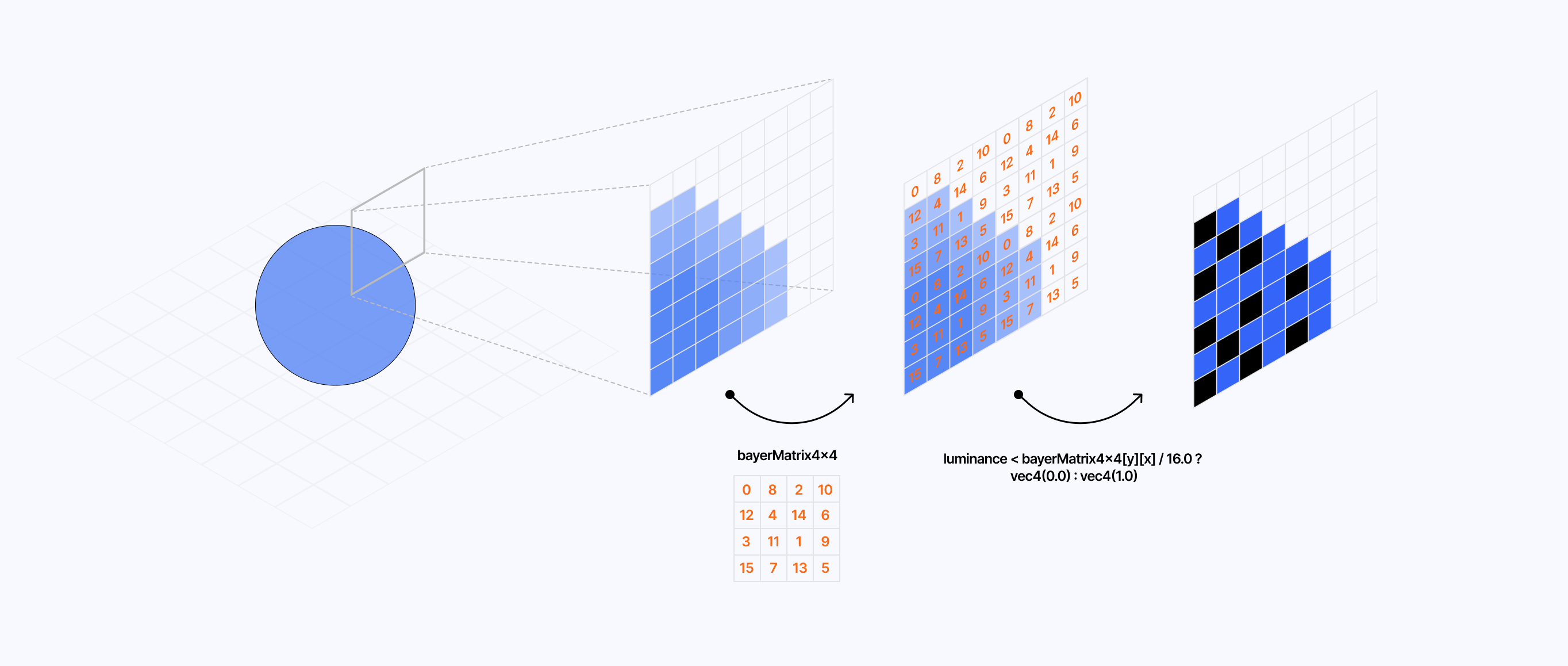
To demonstrate how this dithering type works, I built the widget below where you can see how this matrix changes the output of a grid of pixels once applied on top of it:

As you can see through the examples I showcased above, we get some pretty distinct dithering patterns based on

• the shades of gray used in the underlying pixel grid
• the size of the Bayer Matrix used to get the threshold value

To implement this in GLSL, we need to get the luminance of each pixel and compare its value with the corresponding threshold value for that same pixel obtained from the Bayer Matrix:

• if the difference between those values is positive, the pixel is white
• otherwise, it is black

1
const mat4x4 bayerMatrix4x4 = mat4x4(
2
    0.0,  8.0,  2.0, 10.0,
3
    12.0, 4.0,  14.0, 6.0,
4
    3.0,  11.0, 1.0, 9.0,
5
    15.0, 7.0,  13.0, 5.0
6
) / 16.0;
7

8
vec3 orderedDither(vec2 uv, float lum) {
9
  vec3 color = vec3(0.0);
10

11
  float threshold = 0.0;
12

13
  int x = int(uv.x * resolution.x) % 4;
14
  int y = int(uv.y * resolution.y) % 4;
15
  threshold = bayerMatrix4x4[y][x];
16

17
  if (lum < threshold + bias) {
18
      color = vec3(0.0);
19
  } else {
20
      color = vec3(1.0);
21
  }
22

23
  return color;
24
}

Modifying the effect code we implemented in the previous part with the code we just introduced will give us an ordered dithering effect for our underlying scene:

Blue noise dithering

We got ourselves a satisfying ordered dithering effect! While this is the most popular dithering technique, as well as the main one we'll leverage in this article, I still wanted to touch upon an additonal way to dither that you perhaps remember seeing in my article on Volumetric Raymarching: blue noise dithering.

I used this technique in my raymarched cloud scenes to "erase the banding or layering effect due to a less granular [raymarching] loop" which funny enough is the same use case we need dithering for in our Retro post-processing effect. Unlike the previous techniques, this one relies on a texture that we'll pass to the shader of our custom post-processing effect via a uniform and then sample it as follows:

1
vec4 noise = texture2D(uNoise, gl_FragCoord.xy / 128.0);
2
float threshold = noise.r;

where 128.0 is the width/height of said texture. We also define the threshold as the red color channel of the resulting noise color we obtain from the sampling, given that we're using a grayscale texture, it doesn't matter much which value you pick.

Below is the resulting output when we use a blue noise texture to obtain our dithering threshold value:

As you can see, it feels less repetitive and structured than ordered dithering while also not being as random as white noise dithering; a nice middle ground.

Color Quantization

So far, all our dithering examples also converted the underlying scene to black and white, thus making us lose a lot of information and color. That is because:

• We calculated our dithering threshold based on the pixel luminance, thus relying on a grayscale version of our scene.
• We manually returned a black or white pixel based on the threshold value relative to the luminance.

That technique is commonly referred to as luminance-based dithering and the color conversion used here compresses the color palette to 2-bit: each pixel of the resulting scene with our post-processing effect applied is either black or white, and any shade in-between appears to us through dithering.

This color compression is known as color quantization, and it supports more than just black and white pixels as we'll see in this section.

Shades of gray and colors

Manually setting the colors of our dithering pattern can quickly get out of hand, especially with large color palettes. Instead, to get more than just a black or white pixel and leverage shades of gray, we'll use a formula to find the nearest neighboring color of a given pixel color based on the total number of colors we want to output in our effect:

floor(color * (n - 1) + 0.5)/n - 1 where n is the total number of color.

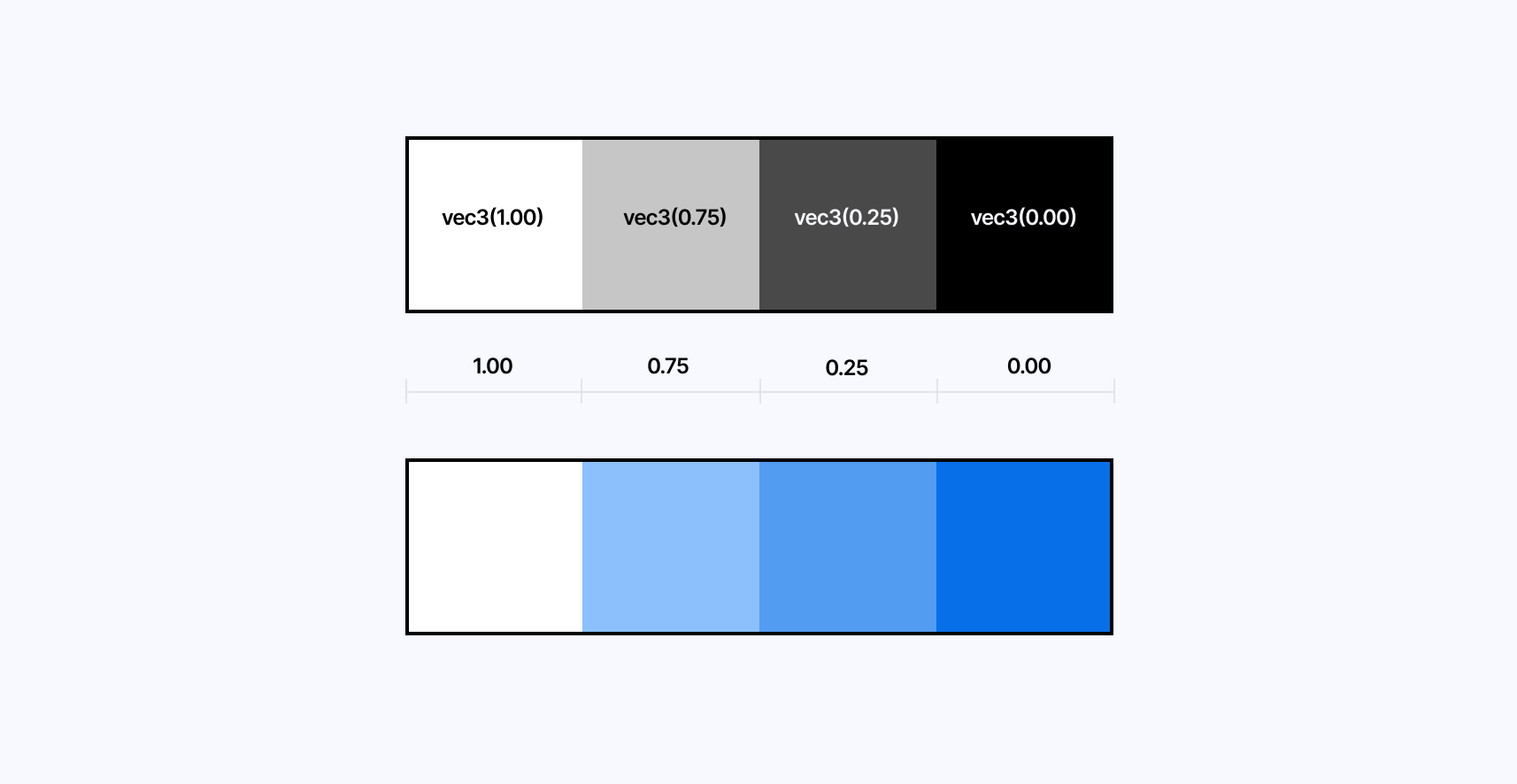
For example, if we wanted only two colors in our final color palette we would get a value of:

• vec3(0.0) for the color vec3(0.3) i.e. black
• vec3(1.0) for the color vec3(0.6) i.e. white

If we were to increase the number of colors we would get more shades of gray in the case of our grayscale scene.

1
vec3 dither(vec2 uv, float lum) {
2
  vec3 color = vec3(lum);
3

4
  int x = int(uv.x * resolution.x) % 8;
5
  int y = int(uv.y * resolution.y) % 8;
6
  float threshold = bayerMatrix8x8[y * 8 + x];
7

8
  color.rgb += threshold;
9
  color.r = floor(color.r * (colorNum - 1.0) + 0.5) / (colorNum - 1.0);
10
  color.g = floor(color.g * (colorNum - 1.0) + 0.5) / (colorNum - 1.0);
11
  color.b = floor(color.b * (colorNum - 1.0) + 0.5) / (colorNum - 1.0);
12

13
  return color;
14
}

This formula doesn't just work for shades of gray, we can use it directly on the original pixel color to compute its nearest neighbor:

• for a two-color palette, we'll get the 2 possible values for each color channel thus 2^3 = 8 colors
• for a four-color palette, it would be 4^3 = 64 colors

1
vec3 dither(vec2 uv, vec3 color) {
2
  int x = int(uv.x * resolution.x) % 8;
3
  int y = int(uv.y * resolution.y) % 8;
4
  float threshold = bayerMatrix8x8[y * 8 + x];
5

6
  color.rgb += threshold;
7
  color.r = floor(color.r * (colorNum - 1.0) + 0.5) / (colorNum - 1.0);
8
  color.g = floor(color.g * (colorNum - 1.0) + 0.5) / (colorNum - 1.0);
9
  color.b = floor(color.b * (colorNum - 1.0) + 0.5) / (colorNum - 1.0);
10

11
  return color;
12
}

This quantization technique lets us approximate the look and feel of older graphics. We can obtain color palettes that are more in line with what computers and consoles could output back in the day.

Custom color palettes

We now know a technique to reduce the number of colors in our final render to an arbitrary number, but what about reducing it to an arbitrary set of colors?

In his video on quantization and dithering, @Acerola_t introduces a technique to do just that by using the value of a grayscale color palette to sample a texture defining a custom color palette.

For example, if our last grayscale example scene from earlier sets the color number to four, we will get the following grayscale values:

These values correspond to the horizontal values of the UV coordinates of our color palette texture, thus letting us use those values to sample the texture and get the custom colors from it:

1
vec3 {13} dither(vec2 uv, float lum) {
2
  vec3 color = vec3(lum);
3

4
  int x = int(uv.x * resolution.x) % 8;
5
  int y = int(uv.y * resolution.y) % 8;
6
  float threshold = bayerMatrix8x8[y * 8 + x];
7

8
  color.rgb += threshold * 0.2;
9
  color.r = floor(color.r * (4.0 - 1.0) + 0.5) / (4.0 - 1.0);
10
  color.g = floor(color.g * (4.0 - 1.0) + 0.5) / (4.0 - 1.0);
11
  color.b = floor(color.b * (4.0 - 1.0) + 0.5) / (4.0 - 1.0);
12

13
  vec3 paletteColor = texture2D(palette, vec2(color.r)).rgb;
14

15
  return paletteColor;
16
}

If we were to apply that technique to the previous scene, this is what the final output would look like:

I'd encourage you to fork this demo and try with:

• different textures
• different number of colors

The only thing to pay attention to is to keep the number of color blocks in your palette texture the same as the number of color you set in your custom effect.

Hue-lightness-based color quantization

In his article Dithering on the GPU Alex Charlton introduces an alternative color quantization technique. Instead of using the quantization formula we introduced at the beginning of this section, he relies on the hue of a color to find its closest neighboring colors from an arbitrary palette and the lightness of those colors to obtain the ordered dithering pattern.

To do so, he proceeds as follows:

1. For each pixel, convert the color to HSL (Hue Saturation Lightness).
2. Find its two closest neighbors in "hue" from the arbitrary color palette defined statically or provided via a uniform.
3. Get the distance between the pixel and its closest color over the distance between the previously obtained colors.
4. Compare this distance with the threshold value from the Bayer Matrix and, based on the result pick the first or second closest color.
5. Get the distance between the two closest lightness that match the original pixel's color.
6. Compare this distance with the threshold value from the Bayer Matrix and, based on the result pick the first or second lightness to set in the final color.

I vividly recommend taking the time to read the full article as it goes in-depth into an original and more artistic dithering process. Below you'll find the demo I re-implemented from the process showcased in the article. It also features some of the missing functions the author did not include in their post.

Pixelization

We now know how to:

• Reduce the number of colors of a given scene to a specific number or an arbitrary color palette.
• Use dithering to get back some of the details of the scene in the form of a dithering pattern like shadows or color gradients.

In this section, we will look at some techniques to downsample the final output of our scene to get a more pixelated look and see our dithering and quantization process shine at lower resolutions.

The key to getting a pixelated version of our original scene is to remap the UV coordinate system used in our effect shader and snap it to a grid so, once sampled, the texture from our input buffer appears as if it were at a lower resolution.

1
void mainImage(const in vec4 inputColor, const in vec2 uv, out vec4 outputColor) {
2
  vec2 normalizedPixelSize = pixelSize / resolution;
3
  vec2 uvPixel = normalizedPixelSize * floor(uv / normalizedPixelSize);
4

5
  vec4 color = texture2D(inputBuffer, uvPixel);
6
  color.rgb = dither(uvPixel, color.rgb);
7

8
  outputColor = color;
9
}

In the code snippet above:

• We define the size of our pixel via the pixelSize uniform.
• We divide this value by the resolution of our scene to convert it to a normalized texture coordinate ranging from 0 to 1.
• We snap the UV coordinate to the grid defined by uv/normalizedPixelSize using the floor function.
• We rescale the snapped UV coordinates to the original UV space by multiplying the result by normalizedPixelSize.

The demo below adds this process along with an additional uniform for you to tweak the pixel size used in our scene:

Notice how the higher the value of pixelSize is, the more pixelated our scene becomes.

On top of that, we can see that our dithering pattern becomes less and less visible as the pixel size increases: there are not enough pixels in the final output to get any pattern at all. We'll have to strike the right balance between dithering pattern and pixel size to get the most compelling effect.

With this added to our effect, we have all the ingredients to produce gorgeous pixel art pieces or pixelated 3D scenes! One thing I immediately tried upon wrapping up this post-processing effect was to try it on top of some of my earlier shader work, like in my scene titled Dithering Waves where I applied a grayscale version of it on top of a simple scene rendering a domain wrapping texture using Fractal Brownian Motion, inspired by Inigo Quilez' article on the matter.

To experiment with contrasting aesthetics, I also wanted to try out ordered dithering and color quantization on some of my Raymarching work from last year. The ordered pattern contrasts nicely with the more organic nature of some of those scenes, especially at lower resolutions. Below are two examples that I particularily enjoyed:

Cathode-Ray Tube effect

While pixelization brings us one step closer to an accurate retro post-processing effect, there is one essential aspect of this effect that's missing: emulating the look of a good ol' CRT monitor.

CRTs work differently than our current displays. Thus, the best we can do here is to approach the look and feel of those old monitors by stacking a series of effects in our custom shader effect. The first and most fundamental effect that we'll work on, that also highlights the inner workings of CRTs, is the RGB cell pattern from the display.

RGB Cells

First and foremost, let's look at how CRT displays work so we can reproduce the effect as accurately as possible. Those monitors have 3 electron guns for each of the color channels (red, green, and blue) that run across the screen and excite their corresponding phosphors, which in return emit light to form an image. To prevent those beams from hitting the wrong phosphor dots and causing color issues on the final image, CRTs use a shadow mask with a metal plate made of tiny holes. They can have many different configurations which yield different mask types.

In this section, we'll attempt to emulate the Schiltzmaske: an aperture grill where each column is staggered by half a cell height.

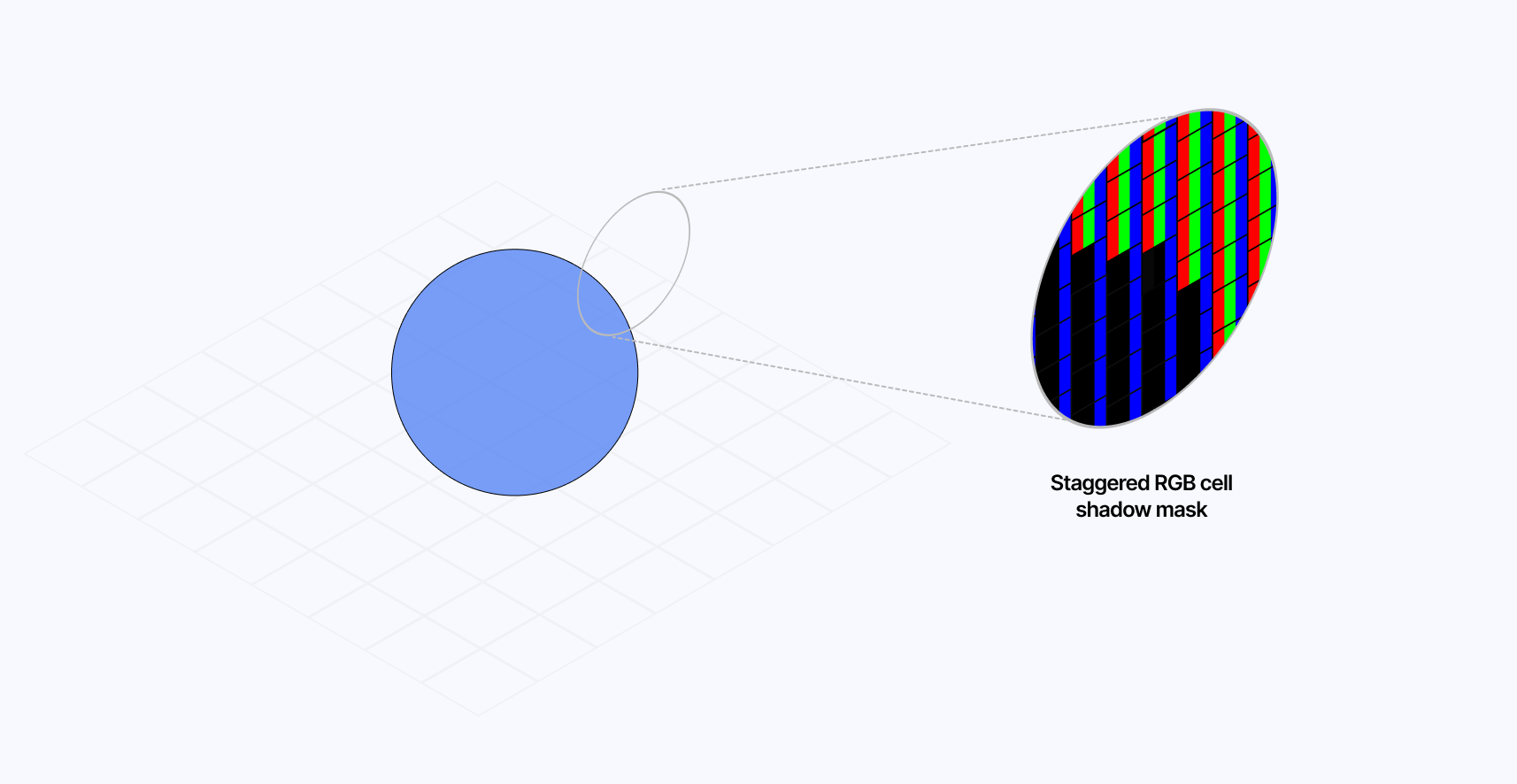
This implementation could also allow us to try to get another mask type called Streifermaske, which is similar except that it does not feature the staggered cells and only features a mask on its column.

The implementation of such a "pixel pattern" in GLSL goes as follows:

• We first need to define our RGB cells and their subcells: a slot for each red, green, and blue channel.

1
vec2 pixel = uv * resolution;
2
vec2 coord = pixel / pixelSize;
3
vec2 subcoord = coord * vec2(3,1);
4
vec2 cellOffset = vec2(0, mod(floor(coord.x), 3.0) * 0.5);

• We create a cell "offset" for every two cells: some will have an offset of vec2(0.0) and some of vec2(0.0, 0.5), thus creating the vertical staggered effect of our shadow mask.

1
vec2 cellOffset = vec2(0, mod(floor(coord.x), 3.0) * 0.5);

• We pick which subcell the current pixel belongs to and output the corresponding subcell color based on the subcell index.

1
float ind = mod(floor(subcoord.x), 3.0);
2
vec3 maskColor = vec3(ind == 0.0, ind == 1.0, ind == 2.0) * 2.0;

• We now need to draw the borders of our masks. The first step is to create a set of UV coordinates for each subcell, then make a border vector that gets higher values in the edges of each subcell and lower towards the center. Finally, we blend the result with the current mask color, thus creating a colored subcell with a border.

1
vec2 cellUv = fract(subcoord + cellOffset) * 2.0 - 1.0;
2
vec2 border = 1.0 - cellUv * cellUv * MASK_BORDER;
3
maskColor.rgb *= border.x * border.y;

• The last step is to create a rgbCellUV vector that we can use to sample the input buffer of our underlying scene and map it in this new CRT RGB Cell coordinate system.

1
vec2 rgbCellUV = floor(coord+cellOffset) * pixelSize / resolution;

This results in a more accurate look and feel for a retro post-processing effect. Those are the types of details that can make the whole difference when making a 3D scene for the web.

The demo below fully implements the process highlighted above, which yields a beautiful and soft CRT effect. Setting a high pixel size will also allow you to admire our subcells at work, lighting up individually based on the color of the underlying scene.

Curving the display

CRTs were not flat like their LCD counterparts. Instead, they featured some slight curvature which we can emulate with a few lines of GLSL. To do so, much like we just did for our RGB cells shadow mask, we can remap our UV coordinates to introduce some curvature:

1
void mainImage(const in vec4 inputColor, const in vec2 uv, out vec4 outputColor) {
2
  vec2 curveUV = uv * 2.0 - 1.0;
3
  vec2 offset = curveUV.yx * curve;
4
  curveUV += curveUV * offset * offset;
5
  curveUV = curveUV * 0.5 + 0.5;
6

7
  //...
8
}

In the code snippet above:

1. We convert our UV coordinates range to a new range of [-1, 1] as we want the curvature to be centered relative to the screen.
2. Swapping the x and y components of our UV coordinates and multiplying by a CURVE_INTENSITY variable lets us define the strength/offset of our curvature. In this case, the offset will be stronger at the corners and not as strong as we reach the center of both the x and y-axis.
3. Finally, we want our curvature to be quadratic, i.e. stronger the closer we get to the fringes of the screen. We then convert the resulting UV coordinates back to a range of [0, 1] allowing us to use it in our shader as the base UVs.

Using those new UV coordinates, we can draw the edges of our CRT using smoothstep:

1
vec2 edge = smoothstep(0., 0.02, curveUV)*(1.-smoothstep(1.-0.02, 1., curveUV));
2
color.rgb *= edge.x * edge.y;

This gives us black curved edges on the top, bottom, left, and right sides of the display. The demo below implements this curvature element to the effect we've been iterating on since the beginning of this blog post and also lets you tweak the curvature intensity from 0 (flat) to 0.5 (realistically curved, anything higher than that is "too much").

Scanlines, distortion, and final touches

In this last part, I wanted to walk you through some of the final touches I added to my own retro post-processing effect to make it as accurate as possible.

One of the first tweaks I felt was necessary was to add some slight chromatic aberration when sampling the input buffer of our effect, which we can find the code of in Refraction, dispersion, and other shader light effects. Due to the screen curvature and some imperfect alignments of the electron beams of the CRT, it was frequent that color channels would appear slightly offset, yielding a slightly blurred image.

1
void mainImage(const in vec4 inputColor, const in vec2 uv, out vec4 outputColor) {
2

3
  //...
4
  vec4 color = vec4(1.0);
5
  color.r = texture2D(inputBuffer, rgbCellUV + SPREAD).r;
6
  color.g = texture2D(inputBuffer, rgbCellUV).g;
7
  color.b = texture2D(inputBuffer, rgbCellUV - SPREAD).b;
8

9
  color.rgb = dither(rgbCellUV, color.rgb);
10
  //...
11
}

Moreover, due to the inner workings of CRTs we highlighted earlier, some Bloom may also occur. We can consider this using the Bloom component from @react-three/postprocessing.

1
const Retro = () => {
2
  const spaceship = useRef();
3
  const effect = useRef();
4

5
  return (
6
    <>
7
      <group rotation={[0, Math.PI / 2, 0]}>
8
        <Spaceship ref={spaceship} />
9
      </group>
10
      <EffectComposer>
11
        <RetroEffect ref={effect} />
12
        <Bloom
13
          intensity={0.25}
14
          luminanceThreshold={0.05}
15
          luminanceSmoothing={0.9}
16
        />
17
      </EffectComposer>
18
    </>
19
  );
20
};

Finally, we can overlay the final output of our custom shader effect with horizontal scanlines running through the screen vertically:

1
float lines = sin(uv.y * 2000.0 + time * 100.0);
2
color *= lines + 1.0;

We can also include some additional distortion to the UV coordinates of our effect by adding code to the mainUv function of our shader. Adding some slight imperfections like these can make our CRT look even more accurate. Below is a simple example, but feel free to further experiment with more complex distortion patterns:

1
float noise (in vec2 st) {
2
  vec2 i = floor(st);
3
  vec2 f = fract(st);
4

5
  float a = random(i);
6
  float b = random(i + vec2(1.0, 0.0));
7
  float c = random(i + vec2(0.0, 1.0));
8
  float d = random(i + vec2(1.0, 1.0));
9

10
  vec2 u = f*f*(3.0-2.0*f);
11

12
  return mix(a, b, u.x) +
13
  (cfloat noise (in vec2 st) {
14
  vec2 i = floor(st);
15
  vec2 f = fract(st);
16

17
  float a = random(i);
18
  float b = random(i + vec2(1.0, 0.0));
19
  float c = random(i + vec2(0.0, 1.0));
20
  float d = random(i + vec2(1.0, 1.0));
21

22
  vec2 u = f*f*(3.0-2.0*f);
23

24
  return mix(a, b, u.x) +
25
  (c - a)* u.y * (1.0 - u.x) +
26
  (d - b) * u.x * u.y;
27
}
28

29
void mainUv(inout vec2 uv) {
30
  float shake = (noise(vec2(uv.y) * sin(time * 400.0) * 100.0) - 0.5) * 0.0025;
31
  uv.x += shake * 1.5;
32
} - a)* u.y * (1.0 - u.x) +
33
  (d - b) * u.x * u.y;
34
}
35

36
void mainUv(inout vec2 uv) {
37
  float shake = (noise(vec2(uv.y) * sin(time * 400.0) * 100.0) - 0.5) * 0.0025;
38
  uv.x += shake * 1.5;
39
}

We're finally done! Or at least I was satisfied enough to make this the stopping point of this article, you can still experiment and continue to tweak this shader at your heart's content! You can admire the final version of our retro post-processing effect below, which includes:

• Color quantization to reduce the number of colors in our final output.
• Pixelization and RGB Cell shadow mask effect to create realistic downsampling typically visible in old CRT displays.
• Ordered Dithering which alleviates the low pixel and color count in the output image and gives us back some details of the underlying scene in the form of pixel patterns.
• Screen Curvature, scanlines with distortions, bloom, and chromatic aberration as final touches to make our effect pop.